Лагранж пăнчи

Лагранж пăнчисем тата икĕ ĕскертен тăракан системăн эквипотенциллă çийĕсем

Лагра́нж пăнчисем, либра́ци пăнчисем (лат. librātiō — суллантару) е L-пăнчăсем тесе икĕ пысăк массăллă ĕскер тытăмĕнчи çавнашкал пăнчăсене калаççĕ, хăшĕсенче шута илмесле пĕчĕк массăллă виççĕмĕш ĕскер, асăннă малтанхи ĕскерсен вăйăмĕнче çеç тăраканскер, çав ик ĕскер тĕлĕшпе ним куçми тăрать. ...................................................................................................................................................................................................................................................................................................................................... Лагра́нж пăнчисем, çаплах вĕсене либра́ци пăнчисем (лат. libratio — суллану, силленӳ) сăмахран е L-пăнчăсем  теççĕ — икĕ йывăрăшлă кĕлетке системинчи пăнчăсем, çак икĕ йывăрăшлă кĕлетке системин гравитаци вăйĕсĕр пуçне шута илмелле мар пĕчĕк йывăрăшлă, нимĕнле вăйсен сĕмне пулман виççĕмĕш кĕлетке асăннă икĕ кĕлетке хушшинче тăнăç тăрăмра пулать.

Тĕп тĕрĕсрех, Лагранж пăнчисем чикĕленĕ виçĕ кĕлетке кăткăсĕн вырăнти тупсăмĕсем пулаççĕ— ун чух пур кĕлеткен орбитисем çавраллă тата пĕрин йывăрăшĕ ытти иккĕшĕнчен пĕринчен чылай çăмăл. Çакăн чухне икĕ пысăк кĕлетке хăйсен пĕрлĕ масса центрĕ тавра пĕр пек кĕтес хăвăртлăхепе çаврăнаççĕ тесе шутлама пулать. Вĕсен таврашĕнчи уçлăхра пиллĕк пăнчă пур, çав тĕлсенче питĕ йывăр кĕлеткесемпе çыхăннă çаврăнакан шутлав системинче çав тери пĕчĕк йывăрлăхлă виççĕмĕш кĕлетке куçăмсăр тăма пултарать. Çак пăнчăсенче пĕчĕк кĕлетке çине яракан гравитаци вăйĕсем варринчен тапакан вăйпа пĕр тан пулса лăпкăланаççĕ.

Лагранж пăнчисем ята Жозеф Луи Лагранж математика чысласа туянтарнă, вăл пĕрремĕш 1772 çулта çак ыйтăва тупсăмпа тивĕçтернĕ.

Лагранж пăнчисен вырнаçăвĕ

Лагранж пăнчисем вырнаçăвне кăтартакан диаграмма

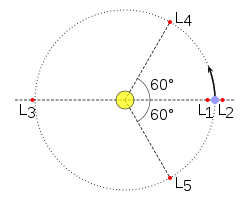
Лагранж пăнчисене L латин пысăк сас паллипе 1-рен пуçласа 5-чен хисеп индексĕпе кăтартаççĕ.

Лагранжăн пур пăнчи йывăр кĕлеткесен орбити лаптăкĕнче выртать. Пĕрремĕш виçĕ пăнчи иккĕш йывăр кĕлетке урлă пыракан йĕр çинче вырнаçнă. Лагранжăн çак пăнчисене коллинеарлисем теççĕ, вĕсене çапла L₁, L₂ и L₃ палартаççĕ.

L₁ икĕ кĕлетке системи хушшинче çăмăлтараххи патнерех вырнаçнă, L₂ — тулти, çăмăлтарах кĕлетке хыçĕнче тата L₃ — йывăртараххи хыçĕнче. Кĕлеткесен системин йывăрăшĕн варри тĕпĕнчен çак пăнчăсене çити пĕрремĕш α-çывхартăвĕпе çак хормулăсемпе шыраççĕ

$r_{1}=R\left[1-\left({\frac {\alpha }{3}}\right)^{1/3}\right]$

$r_{2}=R\left[1+\left({\frac {\alpha }{3}}\right)^{1/3}\right]$

$r_{3}=R\left[1+{\frac {5}{12}}\alpha \right]$

кунта

$\alpha ={\frac {M_{2}}{M_{1}+M_{2}}}$,

R — кĕлеткесем хушши,

M₁ — чи йывăр кĕлеткин йывăрăшĕ,

M₂ — иккĕмĕш кĕлеткен йывăрăшĕ.

Эхер M₂ чылай M₁ пĕчĕкрех, L₁ тата L₂ пăнчисем M₂ кĕлеткерен пĕр пек хушăра тенĕ пекех вырнаçнă:

$r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}$

Лагранж пăнчисенчи Хĕвел системин объекчĕсем

Тепĕр икĕ пăнчи (L₄ тата L₅) пĕр тан енлĕ икĕ йывăр кĕлеткене çыхăнтаракан татăк тĕплĕ виç кĕтеслĕх тăррисенче вырнаçнă. Эхер те çак кĕлеткесен пĕрин йывăрăшĕ теприн йывăрăшĕнчен ытла та пĕчĕк, L₄ тата L₅ пăнчисем пĕчĕк йывăрăшлă кĕлетке орбтити çинче, 60° маларах тата каярах вырнаçаççĕ. Çак пăнчăсене виçкĕтеслĕ е троян пăнчисем теççĕ.

Хĕвел системинчи L₂ пăнчă тĕлĕсем:

• Хĕвел–Çĕр — системинче Çĕртен 1 500 000 çм
• Çĕр–Уйăх — системинче Уйăхран 61 500 çм

Лагранж пăнчисенчи танăçлăх (равновесие)

Ӳкерчĕк:Mira.UV.Accretion.jpg

Иккĕллĕ çăлтăрăн ӳкерчĕкĕ.

Ăслăлăх фантастика ĕçесенче асăнни

Теп статья: Лагранж пăнчи илемлĕ литературăра

Çавăн пекех пăхăр

• Рош хăвăлĕ
• Либраци

Каçăсем

• Точки Лагранжа(акăлч.)
• Точки Лагранжа в научной фантастике 2009 ҫулхи Ҫӗртме уйӑхӗн 29-мӗшӗнче архивланӑ.