Виçкĕтеслĕх

Стандартлă кăтартăш

Виçкĕтеслĕх — 3 тӳпеллĕ (тăрăллă) тата 3 енлĕ чи ансат нумайкĕтеслĕх. Пĕр тӳрĕ йĕр çинче вырнаçман виçĕ пăнчăна татăксемпе çыхăнтарнипе пулнă геометрилле кĕлетке.

Виçкĕтеслĕхĕн тăррисене чылай чухне латтынь пысăк саспаллийĕсемпе (A, B, C), кĕтесĕсене — грек сас паллисемпе (α,β,γ), çав кĕтессене хирĕçле енсене — латтынь пĕчĕк саспаллийĕсемпе (a, b, c) кăтартаççĕ.

Виçкĕтеслĕхĕн танмарлăхĕсем

Виç кĕтеслĕхĕн енĕсеем пĕр-пĕринпе çак танмарлăхсемпе çыхăннă:

• a ≤ b + c
• b ≤ a + c
• c ≤ a + b

Эхер те пĕр танмарлăхĕ танлăхпа тĕл килсен (≤ вырăнĕнче =), виçкĕтеслĕх юхăннă шутланать; малалла пур çĕрте те — юхăнман тĕслĕхсем.

Виç кĕтеслĕхсен тĕсĕсем
Шĕвĕр кĕтеслĕ	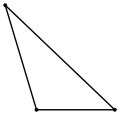Пуклак кĕтеслĕ	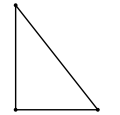Тӳр кĕтеслĕ
Тĕрлĕ енлĕ	Тан аяклă	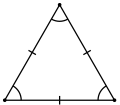Тан енлĕ

Виçкĕтеслĕхĕн палăрăмĕсем

Синуссен теореми

${\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R$

(Теоремăран çак курăнать: a < b < c пулсан, α < β < γ)

Косинуссен теореми

c² = a² + b² — 2ab cos γ

(Пифагор теоремин пĕтĕмĕшли пулать)

Виç кĕтеслĕхĕн кĕтесĕсен суммин теореми

α + β + γ = 180° (π)

Виçкĕтеслĕхĕн лаптăкĕ

Кĕтесĕсене кура

1. $S_{\triangle ABC}={\frac {1}{2}}bh_{b}$, так как $\ h_{b}=a\sin \gamma$, то:
2. $S_{\triangle ABC}={\frac {1}{2}}ab\sin \gamma$
3. $S_{\triangle ABC}={\frac {1}{2}}r(a+b+c)=pr=(p-b)r_{b}$
4. $S_{\triangle ABC}={\frac {abc}{4R}}$
5. $S_{\triangle ABC}={\sqrt {p(p-a)(p-b)(p-c)}}={1 \over 4}{\sqrt {(a+b+c)(b+c-a)(a+c-b)(a+b-c)}}$ — Герон формули
6. $S_{\triangle ABC}={\frac {a^{2}\sin \beta \sin \gamma }{2\sin \alpha }}$
7. $S_{\triangle ABC}={2R^{2}\sin \alpha \sin \beta \sin \gamma }$
8. $S_{\triangle ABC}={\frac {1}{2}}{\begin{vmatrix}x_{A}&y_{A}&1\\x_{B}&y_{B}&1\\x_{C}&y_{C}&1\end{vmatrix}}={\frac {\left|x_{A}(y_{B}-y_{C})+x_{B}(y_{C}-y_{A})+x_{C}(y_{A}-y_{B})\right|}{2}}=$
   $={\frac {\left|(x_{B}-x_{A})(y_{C}-y_{A})-(x_{C}-x_{A})(y_{B}-y_{A})\right|}{2}}$
9. $S_{\triangle ABC}={\frac {ab}{2}}=r^{2}+2rR$ — тӳркĕтеслĕ виç кĕтеслĕх валли
10. $S={\frac {a^{2}{\sqrt {3}}}{4}}$ — пĕр тан енлĕ виç кĕтеслĕх валли
11. $S_{\triangle ABC}={\frac {c^{2}}{2(ctg\alpha +ctg\beta )}}$ — енчен виç кĕтеслĕхе енĕпе тата ун патĕнчи икĕ кĕтеспе палăртсан
12. $S_{\triangle ABC}={\frac {c^{2}\sin \alpha \sin \beta }{2sin(\alpha +\beta )}}$ — енчен виç кĕтеслĕхе енĕпе тата ун патĕнчи икĕ кĕтеспе палăртсан

Ăçта:

• $\ h_{b}$ — $\ b$ енне антарнă çӳллĕш,
• $p={\frac {a+b+c}{2}}$ — çур периметр,
• $\ r$ — шал çавракăшăн радиусĕ,
• $\ R$ — тул çавракăшăн радиусĕ,
• $\ (x_{A},y_{A});(x_{B},y_{B});(x_{C},y_{C})$ — виç кĕтеслĕх тăррин координачĕсем.

Виçкĕтеслĕхĕн кĕтесĕсен сумми 180° тан пулнипе, виçкĕтеслĕхĕн ытти икĕ кĕтесĕ шĕвĕрлĕ (90° сахал) пулмалла. Çак тĕссене палăртаççĕ:

• Эхер виçкĕтеслĕхĕн пу кĕтесĕсем шĕвĕр, вара виçкĕтеслĕхе шĕвĕрк ĕтеслĕ теççĕ;

• Эхер виçкĕтеслĕхĕн пĕр кĕтесĕ пуклак (90°-ран пысăкрах), ăна пуклак кĕтеслĕ теççĕ;

• Эхер виçкĕтеслĕхĕн пĕр кĕтесĕ тӳрĕ (90° тан), ăна тӳрĕ кĕтеслĕ теççĕ. Тӳре кĕтес тавакан икĕ енĕсене катетсем, тӳрĕ кĕтесе хирĕслĕ енне гипотенуза теççĕ.

Çавăн пекех пăхăр

• Виç кĕтеслĕхĕн кĕтесĕсен суммин теореми
• Синуссен теореми
• Косинуссен теореми
• Герон формули
• Виçкĕтеслĕхĕн чаплă пăнчисем

Каçăсем

• Виç кĕтеслĕх элеменчĕсене шутласси