Октаэдр

Октаэдр
Пысăклатма, сăнне шаклаттарăр. Фигира çаврăннине курас тесен кунта шаклаттарăр.
Тĕс	Терĕс нумайхысаклăх
Хысак	виçкĕтеслĕх
Хысаксем	$8\,\!$
Аяк пĕрчисем	$12\,\!$
Тăрăсем	$6\,\!$
Тăрă çумĕнчи хысаксем	$4\,\!$
Аяк пĕрчин таршшĕ	$a\,\!$
Çий лаптăкĕ	$2a^{2}{\sqrt {3}}\,\!$
Калăпăш	${\frac {1}{3}}{\sqrt {2}}a^{3}$
Тулашпе çырнă сфера радиусĕ	${\frac {a}{2}}{\sqrt {2}}$
Ăшне çырнă сфера радиусĕ	${\frac {a}{6}}{\sqrt {6}}$
Симметри пăнчă ушкăнĕ	Октаэдр (Oh)
Иккĕллĕ нумайхысаклăх	Куб

Октаэдр сарăмĕ

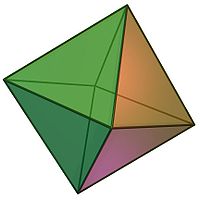
Окта́эдр (грек οκτάεδρον, грек οκτώ, «саккăр» тата грек έδρα — «тĕп, никĕс») — пиллĕк мăкăрăлчăк тĕрĕс нумайхысаклăхран пĕрри, Платон кĕлетки ятлăскер.

Октаэдр 8 виçкĕтеслĕ хысак, 12 аяк пĕрчиллĕ, 6 тăрăллă, кашни тăрринче 4 аяк пĕрчи тĕкĕшкççĕ.

Октаэдр аяк пĕрчин тăршшĕ а тан пулсан, унăн çийĕн лаптăкĕпе (S) калăпăшне (V) çак формулăсемпе шыраççĕ:

$S=2a^{2}{\sqrt {3}}$

$V={\begin{matrix}{1 \over 3}\end{matrix}}{\sqrt {2}}a^{3}$

Октаэдр тулашĕпе çырнă сфера радиусĕ:

$r_{u}={\frac {a}{2}}{\sqrt {2}}$,

Октаэдр ăшне çырнă сфера радиусĕ:

$r_{i}={\frac {a}{6}}{\sqrt {6}}.$

Терĕс октаэдр симметрийĕ кубăн пекех O_h.

Октаэдр çутçанталăкра

• Çутçанталăкри чылай куб кристаллĕсем октаэдр ĕлкиллĕ. Ку алмаз, натри хлоричĕ, перовскит, оливин, флюорит, шпинель.
• Таса металсен (никкĕл, пăхăр, магни, титан, лантан) тата нумай ион çыхăнăвĕсен ((натри хлоричĕ, сфалерит, вюрцит тата ыт.) тачă структурин октаэдр ĕлкинче атом хушшинчи пушăсем пур.

Çăлкуçсем

• Пысăк совет энциклопедийĕ