Иррационаллă хисеп

π — иррационаллă хисеп

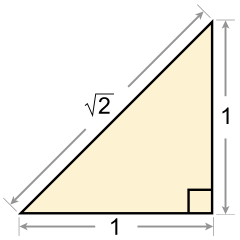
Иррационаллă хисеп — рационаллă мар чăн хисеп. Çапла вара ăна $\pm {\frac {m}{n}}$ ахаль вак пек кăтартма май çук, — кунта $m,n$ — натураллă хисепсем

Иррационаллă хисепе вĕçĕмсĕр тăсăлакан периодла мар вуншарлă вак пек кăтартма пулать.

Урăхла каласан, иррационаллă хисепсен йышĕ $\mathbb {I} =\mathbb {R} \backslash \mathbb {Q}$ , — чăн хисепсен йышĕнчен рационаллă хисепсен йышне кăларни.

Вуламалли

В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — 672 с. — ISBN 5-482-00445-7.
История математики с древнейших времен до начала XIX столетия. В трех томах / под ред. Юшкевича. — М.: Наука, 1970.
Kline, M. (1990). Mathematical Thought from Ancient to Modern Times, Vol. 1. New York: Oxford University Press. (Original work published 1972).
Matvievskaya, Galina. The Theory of Quadratic Irrationals in Medieval Oriental Mathematics (англ.) // Annals of the New York Academy of Sciences (англ.)русск. : journal. — 1987. — Vol. 500. — DOI:10.1111/j.1749-6632.1987.tb37206.x.
Kurt Von Fritz. The Discovery of Incommensurability by Hippasus of Metapontum (англ.) // The Annals of Mathematics : journal. — 1945.

Каçăсем

Zeno's Paradoxes and Incommensurability 2016 ҫулхи Ҫу уйӑхӗн 13-мӗшӗнче архивланӑ. (n.d.). Retrieved April 1, 2008

п • с • т Хисепсен системисем
Шутла йышсем	Натураллă хисепсем ( $\scriptstyle \mathbb {N}$ ) • Туллисем( $\scriptstyle \mathbb {Z}$ ) • Рационаллисем ( $\scriptstyle \mathbb {Q}$ ) • Алгебрăллисем ( $\scriptstyle {\overline {\mathbb {Q} }}$ ) • Периодсем • Шутлавлисем • Арифметикăллисем

Чăн хисепсем тата вĕсен анлăлатăвĕсем	Чăннисем ( $\scriptstyle \mathbb {R}$ ) • Комплекслисем ( $\scriptstyle \mathbb {C}$ ) • Кватернионсем ( $\scriptstyle \mathbb {H}$ ) • Кэли хисепĕсем (октавăсем, октонионсем) ( $\scriptstyle \mathbb {O}$ ) • Седенионсем ( $\scriptstyle \mathbb {S}$ ) • Альтернионсем • Дуаллисем • Гиперкомплекслисем • Вышкайсăр чăннисем • Гиперчăннисем • Сюрреаллисем

Хисепсен системисене анлăлатмалли инструментсем	Кэли — Диксон процедури • Фробениус теореми • Гурвиц теореми

Хисепсен ытти системисем	Кардиналлă хисепсем • Йĕрке хисепĕсем (трансфинитлисем, ординалсем) • p-адиллисем • Вышкайсăр натураллă хисепсем • Интервалла хисепсем

Çав. пекех	Гиперболăлла хисепсем • Иррационаллă хисепсем • Трансцендентлă хисепсем • Хисепсен пайăрки • Бикватернион